Mathematical Fluid Mechanics: Predicting the Properties of Flow

Imagine an industrial factory line – not a flat one, but slightly inclined. Paint is flowing down the line. A technician adds a chemical called a surfactant. Will the paint continue moving smoothly or become disturbed by waves?
Most people will never contemplate such theoretical questions. Yet, the answers will almost certainly impact them in some way, at some time. From industrial metal coatings and mountain mud slides to lubricating eye drops and moulded chocolate confections, the properties and behaviours of flowing substances have everyday applications.
The field is fluid mechanics and it’s been Eglal Ellaban’s mathematics specialty for years. Most recently, the Ryerson PhD student published a paper (external link) in Physical Review Fluids with supervisor, Jean-Paul Pascal and collaborator Serge J.D. D'Alessio (external link) of the University of Waterloo. Together, the researchers uncovered new truths about a scenario similar to the one described in the outset.
Mathematical Equations to Model Flow
Fluids react in different ways to different factors. Temperature, surface conditions and speed are just a few of the variables that influence how a liquid or gas moves and changes. Understanding these behaviours goes beyond pure academic exercise. It’s the key to predicting, managing and controlling fluid flows in all sorts of contexts – environmental, chemical, biomedical, manufacturing and more.
While fluid flows happen in the real, physical world, mathematicians like Ellaban can study the phenomena without using tangible models. Instead, mathematical models can be built on the numbers and analyses. “You can study fluids from a physics or a math perspective,” Ellaban explains. “With math, it’s about creating equations that describe each of the various parameters, and then connecting them all into a solution that predicts what will happen in that specific scenario.”
Although in rare cases, waves and perturbations in fluid flows may be beneficial, Ellaban cites the ideal: “In almost all scenarios, we want surfaces to be stable. We don’t want waviness or variations in thickness. Even when covering biscuits in chocolate, you typically want a smooth surface. So, we might study the properties of chocolate, of heat and other factors, and then figure out when and how it may become unstable.”
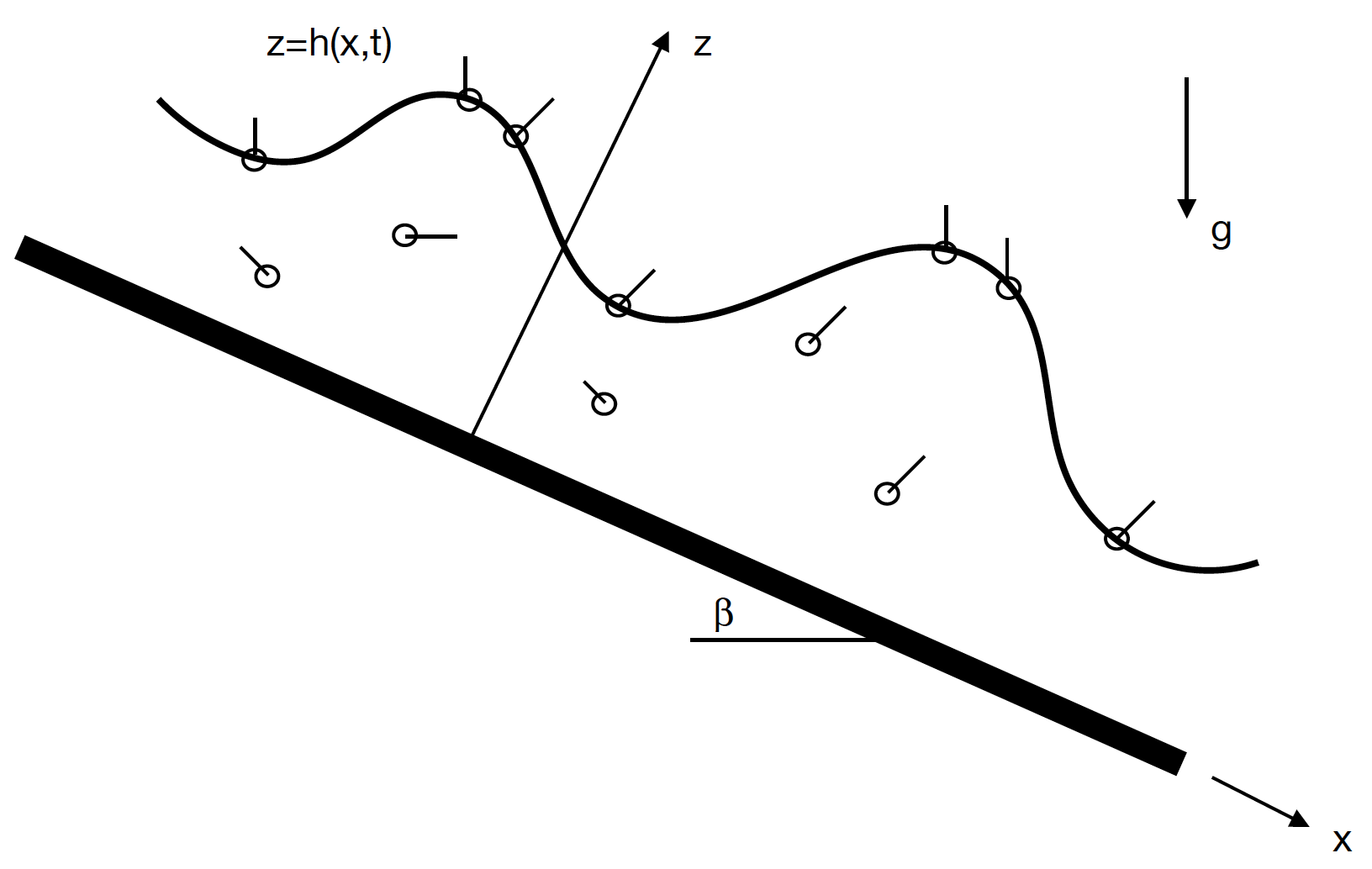
Schematic representation of a thin film flowing down an inclined plane
Surfactant-Spiked Liquids on an Incline
In her published work, Ellaban imagined a scenario involving a few distinct parameters: a thin, liquid film flowing down an incline, driven only by gravity, and spiked by a soluble surfactant.
Surfactants are often used in detergents, conditioners, paints, lubricants and other products. When added to a liquid layer they are adsorbed to the surface and weaken surface tension. They can also dissolve into the bulk of the layer thus affecting the concentration on the surface and also making the liquid in the bulk denser. Both variables – changes in surface tension and mass density – can influence fluid motion, waves and stability.
Ellaban’s challenge was to create a theoretical math model that accounts for all of these parameters. She explains the end goal: “We want to predict what will happen if we add more surfactant, and then determine the critical point when the flow changes from stable to unstable.”
The published paper features an impressive collection of mathematical equations and derivations, with various results for different cases. Ellaban provides a filtered summary of their findings: “We found that in general, adding a surfactant stabilizes the flow, but only at first. As we add more surfactant, desorption to the bulk becomes more significant, altering the distribution of surfactant on the surface and eventually creating instability.”
Further Investigation into the Nuances of Fluids
While Ellaban’s results may seem abstract, her mathematical models may yet be used in a variety of future contexts and applications involving fluids and surfactants. Meanwhile, she’s now exploring a new scenario in flow of fluid layers: What happens if surfactants are added to a heated mixture of different liquids?
“When I explain my work to people, they may struggle to see its usefulness because applications aren’t obvious,” she says candidly. But for Ellaban and fellow scientists, the mathematical secrets underlying fluid dynamics continue to fascinate. She concludes: “Once the work is published and others cite it, you feel you’re helping society by contributing more knowledge. That makes us mathematicians happy and satisfied.”
Ellaban’s research was funded by NSERC.